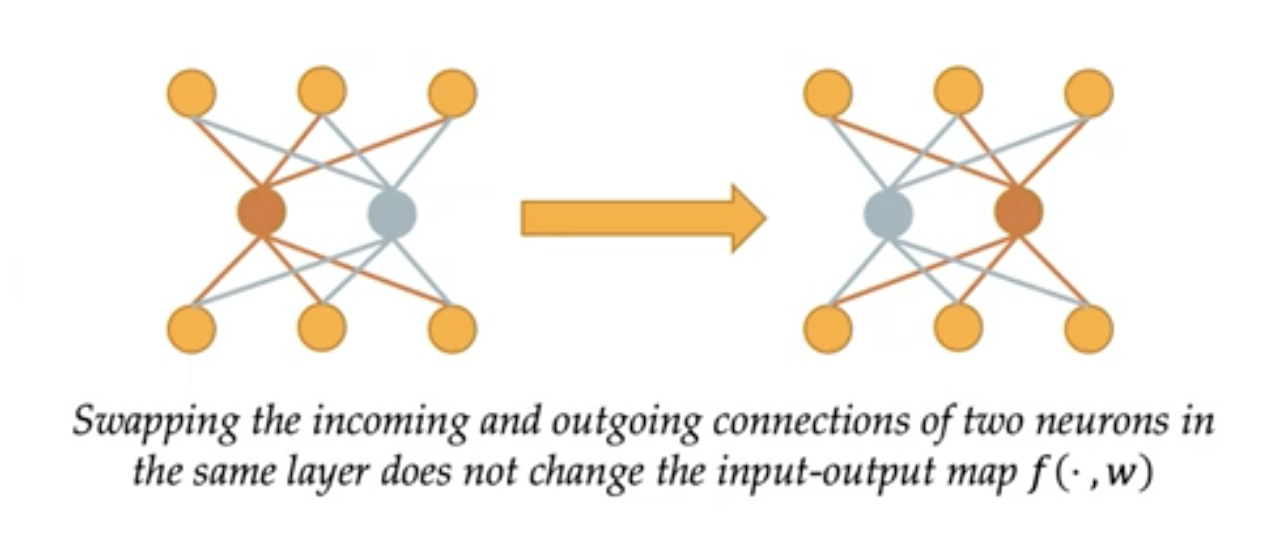
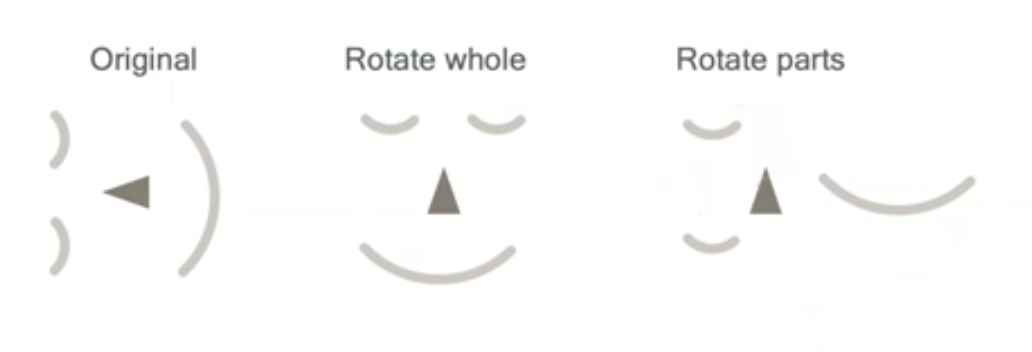
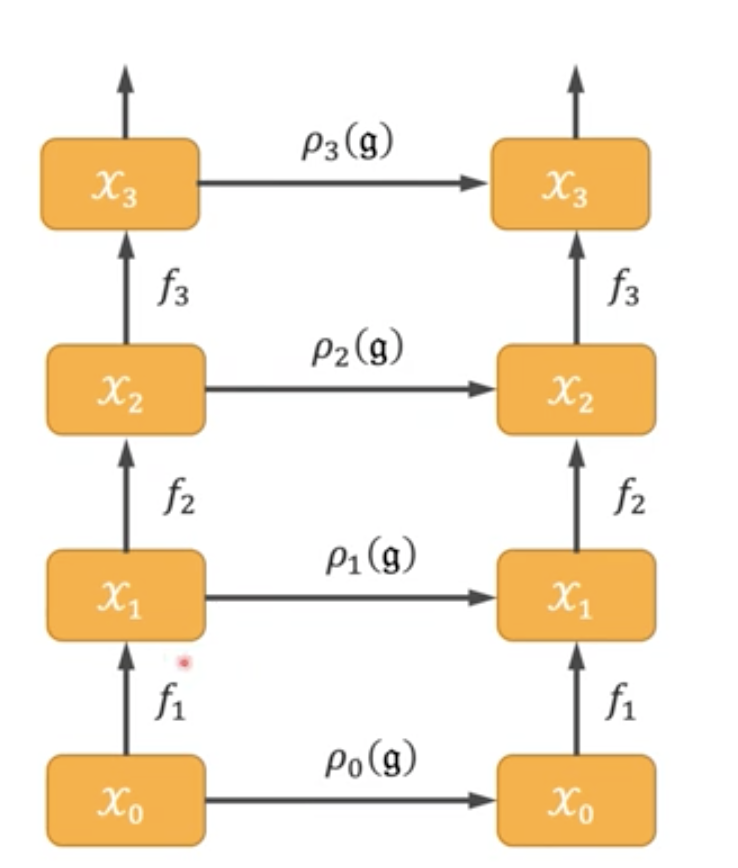
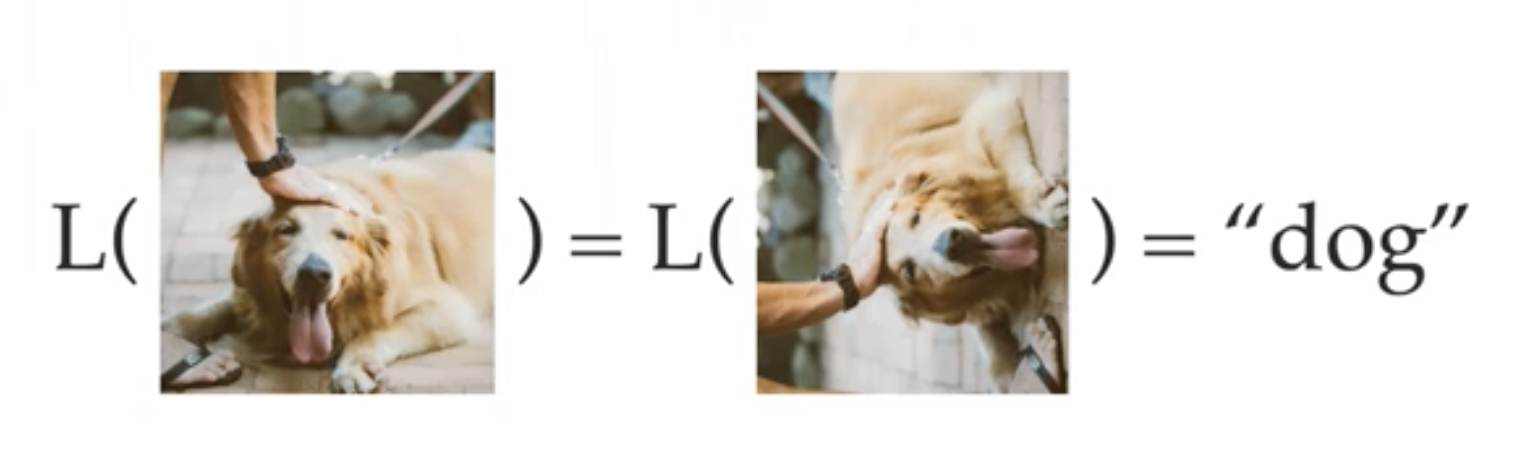Yes, abstract algebra is actually useful for machine learning.
Introduction
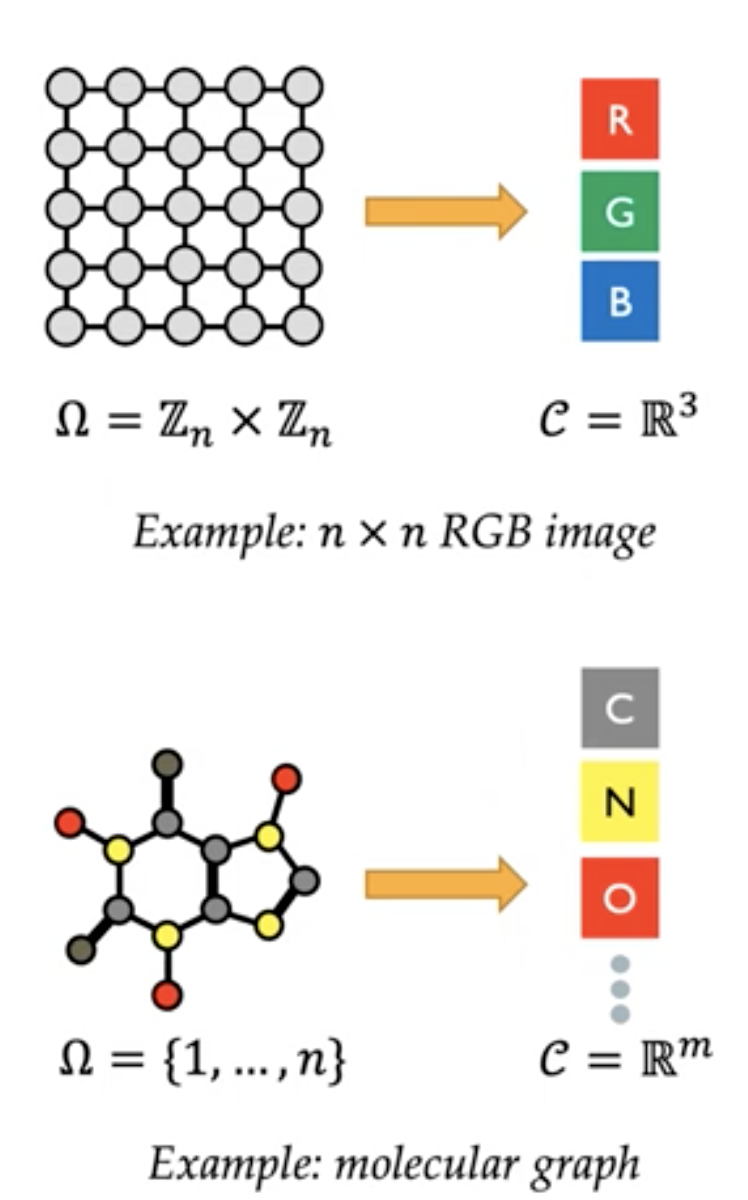
Machine learning operates on images, text, speech and much more. We intuitively understand that they include structure, but for most of us, this is where our knowledge stops. With the emergence of geometric deep learning, there is an increased need to understand the invariances, symmetries in the data.
When I started my B.Sc. in electrical engineering at the Budapest University of Technology and Economics in 2015, the curriculum of our “Introduction to Computer Science” class was changed; it no longer included abstract algebra. Looking into the assigned book, I thought this to be a reasonable decision, as I could not imagine myself using groups, rings, or bodies. I still think that this was a reasonable decision for most students, but I have realized that I missed a great opportunity to understand a deeper level of mathematics, and a way to connect to the real-world.
The name “abstract algebra” and connections to the real world seem to be controversial, but I think they are not. Though having a “rotation” is more abstract than a matrix in the mathematical sense, it is a concept we can easily relate to. When I think about rotation matrices, I always associate the physical rotation in three dimensions to have an easy-to-grasp mental concept for the mathematical description. You might object that this only works in 3D. Yes and no: though I only have access to the real-world meaning of rotations in 3D, but through this I have a general idea about what rotations are, so I am not baffled when I hear about 100-dimensional objects being rotated.
Geoffrey Hinton’s sarcastic remark also highlights our brain’s capacity to handle complex scenarios:
To deal with a 14-dimensional space, visualize a 3-D space and say ‘fourteen’ to yourself very loudly. Everyone does it.
In abstract algebra, we deal with sets and equip them with different relationships and properties, which we will describe with the help of operations. Operations take a number of elements from a set and map they to another element in the set. We can distinguish unary (acts on one element), binary (acts on two elements), tertiary, etc. operations.
This is the same concept you know from programming, so we can think of them as functions with a given number of inputs. Negating a boolean is a unary operator (as it changes the value of a single variable, it is a function with one input), but adding two numbers is binary (two inputs, but still one output).
In mathematics, we can describe such functions as operations mapping from a sequence of elements of a set $S$ (i.e., we take 2 elements from $S$ for a binary operator) to another element in $S$.
In the case of addition (for integers in this example), the Python type hints describe $S$, and we can see that our function maps $S\times S \to S$, meaning that the first parameter x comes from the set int, and so does y. As a result, we get another int with the value x+y.
def add(x:int, y:int)->int:
return x+y
An operation is a function,
and as one, it can have different properties. These properties are the instructions how we can apply the operators (functions), and have a role in what symmetries are present in $S$.
- Associativity: the binary operator * is associative if it admits the rearrangement of parenthesis (i.e., the order of carrying out the operations). Thus, $a*(b*c)=(a*b)*c$.
- Commutativity: the binary operator * is commutative if its arguments are exchangeable (i.e., if they can switch place). Thus, $a*b=b*a$.
* is used as a symbol for an arbitrary operator, it does not necessarily mean multiplication.
Abstract algebraic structures are defined by the set $S$, an operator/operators and their properties. They form a hierarchy, where we get more and more valid operations. This means that more complex structures admit more “exotic” functions. Intuitively, this equals of having richer “representations” (in the machine learning sense).
Before advancing through this hierarchy, we should ponder the question: if we can have richer representations, why would be satisfied with simpler ones? That is, why do we need simpler algebraic structures?
Complexity has its price. Thinking in terms of neural networks, a larger model is more powerful, but is harder to train, whereas the smaller one is faster, but less expressive. A convolutional network is invariant to translations, which is useful for images, but could be useless or harmful in other contexts. As we would not choose a huge model for MNIST (we would risk overfitting), we select the simplest algebraic structure that admits the properties we want. In the following, we describe our choices.
Groups
Groups are already special, they have specific prperties (see below). To provide some perspective, we start with a very simple structure comprising of a set and a simple associative operation. It is not much, though it deserves its own name:
A set $S$ is an associative semigroup if it has an associative operator *. If * is also commutative, we call it a commutative (or abelian) semigroup.
$n\times n$ matrices are a good example for associative semigroups. They can describe linear transformations, such as rotations, translations, so even this simple structure is powerful. Though they are not abelian as matrix multiplication is generally not commutative. This means that selecting the set of matrices that commute w.r.t. * is a smaller set.
Having defined an algebraic structure, we can interpret what we mean by the operator mapping $S\times S\to S$: multiplying two $n\times n$ matrices will also be an $n\times n$ matrix. That is, $S$ is closed w.r.t. *. This is not the case for all operators. If our operator is the subtraction, then $S=\mathbb{N}$ is not a group (w.r.t -), as $(7-9)\not\in\mathbb{N},$ which violates that the result of the operator (the output of the function) should be in the same set. In this case, enlarging $S$ is the solution. If we choose $S=\mathbb{Z}$, then $S$ is closed w.r.t. subtraction.
If we demand that the $S$ contains a unit element (identity) w.r.t. the operator *, then we call $S$ a monoid. It is important that we speak about “identity w.r.t. the operator *”, as we will see that more complex algebraic structures can have multiple operators and so multiple identity elements. An example is the identity matrix $I_n$ for the set of $n\times n$ matrices and the matrix multiplication *. In this case, we can call $I_n$ a multiplicative unit element to differentiate it from other possible unit elements.
A set $S$ is a group with the operator * if:
- * is associative
- has an identity element $i$ s.t. $\forall x \in S : x*i = i*x = x$
- the inverse of each element is unique and is also in $S$, i.e., $\forall x\in S \implies y \in S : x*y=y*x=i$
The leap from monoids to groups is the existence of the inverse element. Though this can seem as an unimportant feature, it is not. Namely, having the inverse means in $S$ means that we can undo the operation (think about this as the option of Ctrl+Z/Cmd+Z on your laptop). That is, we can answer the question: What was the starting point before applying a specific element? In the machine learning perspective, if we assume that our data is generated by latent factors, then we will be able to recover them. As for semigroups, we can define commutative/abelian groups if * is also commutative.
Grouping groups
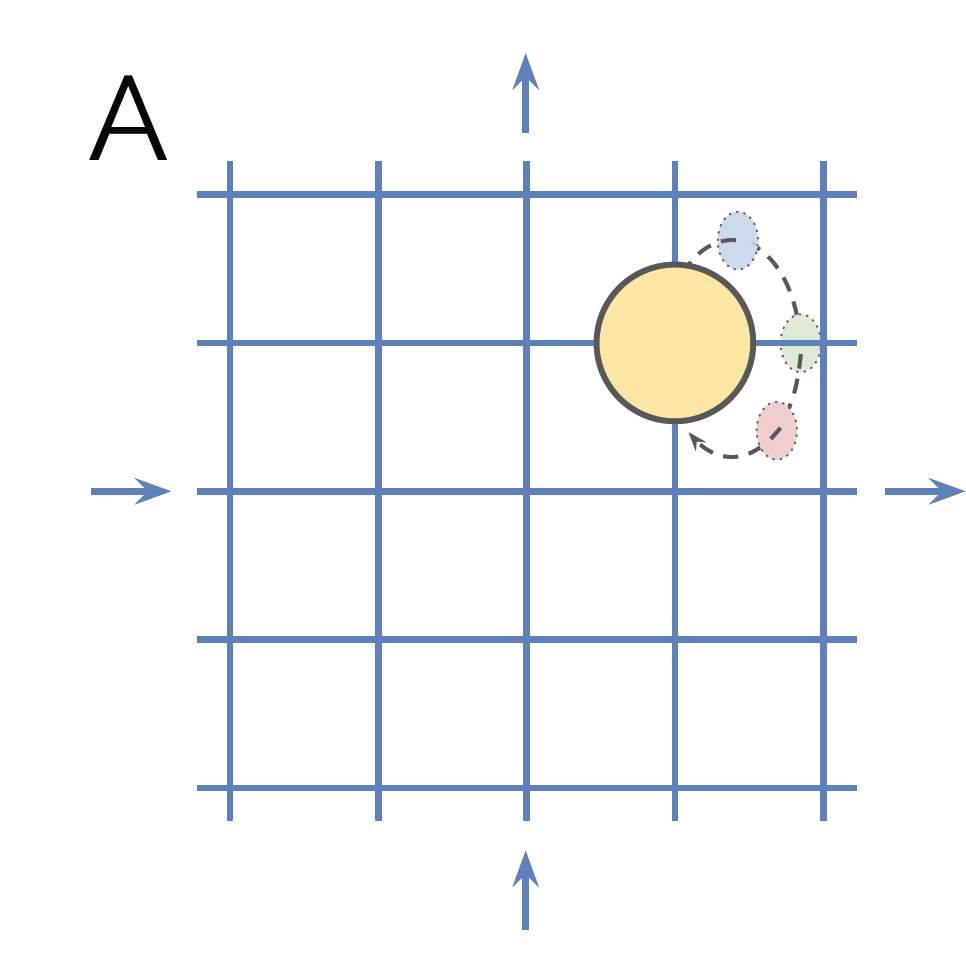
When we have images with different shapes, positions, and colors it is useful to build categories like triangles, circles, and squares. These are subgroups of the original group. That is, if our group $G$ contains vectors with elements $[x; y; angle; shape, color]$ and the operator * combines the features (e.g., translates the object) then a subgroup is a set of elements where some coordinates of the feature vector are fixed. Triangles are elements where $[x; y; angle;shape=triangle, color]$ and so on.
So a subgroup is a subset $S$ of the elements with the same operator as the group $G$. This is like a specific 2D plane in 3D space.
Note that subgroups need to contain the identity of the group to have inverses.
Subgroups are useful as they correspond to how we would categorize objects. We think about triangles, circles, and squares as distinct objects. If we would like to cover the whole space of objects, i.e., to get a description of all 2D planes covering 3D space, we need the concept of cosets.
Cosets describe a set of subgroups $S$ that cover the original group $G$.
For 2D planes parallel to the $x-y$ plane of the Cartesian coordinate system, this means having all translations along the $z$ axis. This idea is generalized by taking an element of $g\in G$ and applying the group operator * on $g$ and all $s\in S$. That is, we shift all points of the plane ($S$) with $g$. The concept is captured mathematically as $S*g,$ where this means that we take all $s\in S$ and apply * with a single $g\in G$ (this yields a single 2D plane, shifted by the vector $g$ for all $s\in S$); then you repeat it for every $g$ (to cover the whole 3D space). We can generate subgroups both as $s*g$ (right coset) and $g*s$ (left coset), but we will only focus on cases when both are the same, which we will call normal subgroups. An intuitive way to think about this is to compare this property to commutativity.
How do we benefit from dividing groups into smaller entities besides having a more intuitive description?
This enables us to express certain symmetries. Take rotations of objects for example. They are a describe a subset of objects with different orientation. So we write a function to to render objects with all rotations. As our computational power is finite, we need to define a step size for the angle. Make it to $1^\circ$. In this case, the rotation element $R_1$ (“rotate by $1^\circ$”) generates a subgroup (as our group contains other features such as position, shape, etc.) containing $R_1, R_2, \dots, R_{359}, R_{360}$. You need all 360 elements, otherwise the group operator (multiplying the rotation matrices) would create elements not in the subgroup. Moreover, this subgroup is cyclic. When we apply $R_1$ consecutively, we will not get an infinite amount of different elements as $R_{360}=R_0$ (the identity). We call the smallest number of applying the generating element $R_1$ and getting back the identity as the order of the subgroup.
Normal subgroups can be used to define another group, called factor or quotient group, denoted by $G/S$. The name “quotient” comes from an analogy to division: as quotient groups are sets of cosets of $S$, this means that a quotient describes a “clustering” of $G$ according to $S$. Namely:
- $S$ has its cosets w.r.t $G$ that cover $G$ with non-overlapping subgroups;
- $G/S$ collects all such subgroups together;
- the implication is that the order of the quotient group, $|G/S|$ is the number of cosets of $S$.
The last point illustrates the additional information conveyed by quotient groups compared to plain old division: division only gives the order (i.e., the quotient), but quotient groups provide the elements too. An example is taking the positive integers as $G$ with addition as the group operation and defining the normal subgroup as the numbers that are the multiple of e.g. $7$. This means that $G/S$ will give the integers modulo $7$, i.e., it divides all positive integers into $7$ clusters, those with the remainder $0,1,2,3,4,5,6$ w.r.t. division by $7$.
Regarding technical details, the group structure follows from the properties of normal subgroups, namely, that the left and right cosets are the same. For $S*g = g*S $, we can rewrite this as $S=g^{-1}*S*g$. From the equivalence of left and right cosets follows that $S$ is the unit element of the factor group, since $S*(g*S)=S*(S*g)$ and $S*S=S$; thus $S*(g*S)=S*(S*g)=S*g$. By left-multiplying with $S$, we can notice that $S*S=g^{-1}*S*g=S,$ so we have an inverse too.
From a machine learning perspective, we can see the merit of factor groups, as they can express how different elements in a (data) set are grouped together, e.g., this is what we want when clustering data.
Expressing group equivalence (isomorphism)
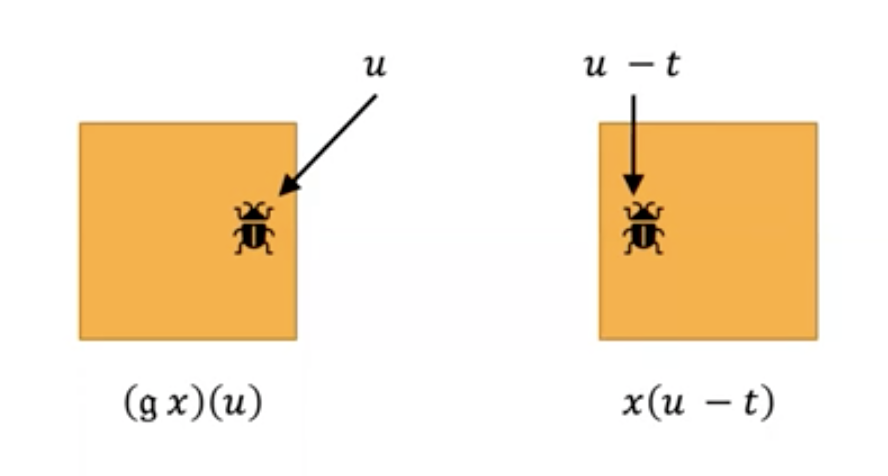
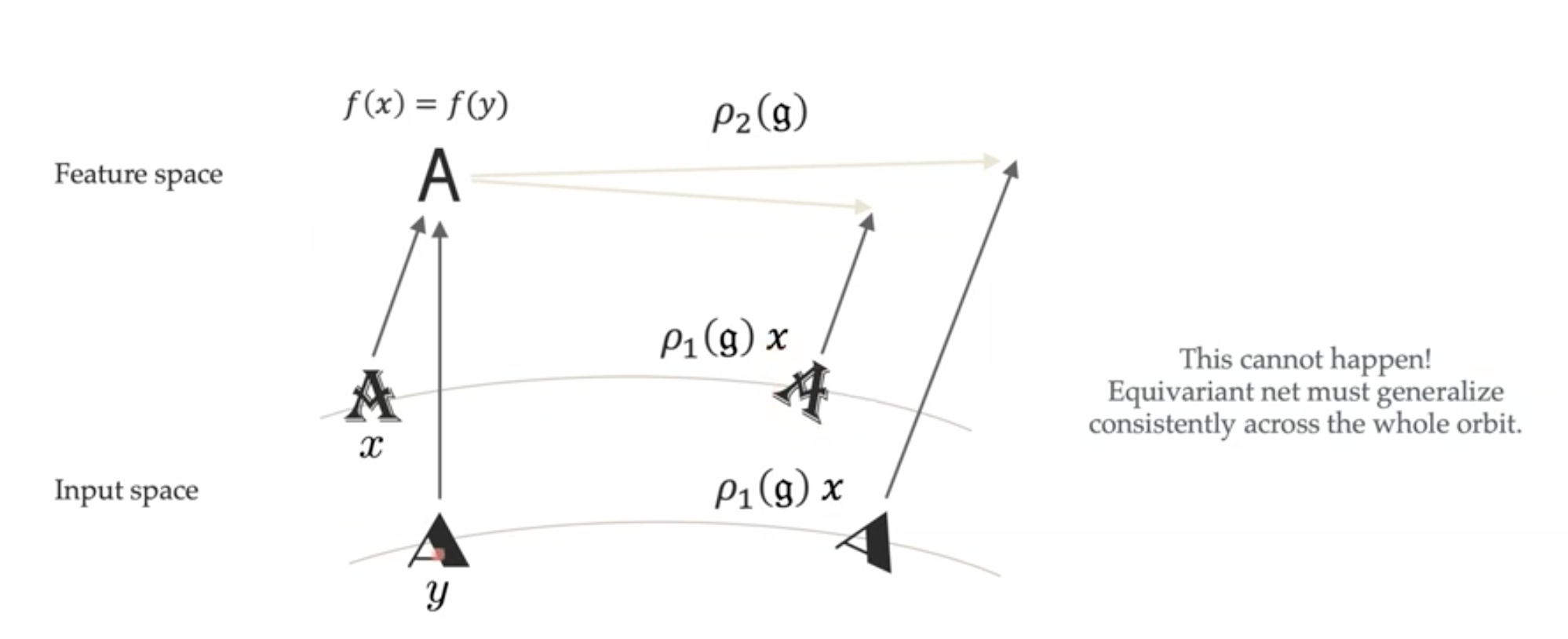
We can describe the same group with different representations. If we have an image, it does not change its meaning if we select the top left or the bottom right pixel as the origin of our coordinate system. For we can find a bijective mapping that transforms the coordinates from one frame to the other. This notion, which we call isomorphism, is important as it reduces the number of different sets (as we only need to take care of those that are not isomorphic to each other, e.g., we don’t need to have all coordinate systems for our images).
Formally, two groups $G_1, G_2$ are isomorphic if there is a bijective mapping $\phi: G_1 \to G_2$ such that $ \forall x,y \in G_1 : \phi(x)*\phi(y) = \phi(x*y)$, where * is the group operation.
The definition says that if we apply the group operation to two elements in $G_1$, then map the resulting group element to $G_2$, we get the same result as applying the group operation of $G_2$ to the elements that are mapped to $G_2$. Going back to our representation learning example, let’s assume that the operator in $G_1$ (the latent space) “combines the features” (similar to + for numbers, e.g., if $x$ describes a red triangle and $y$ a blue triangle, then $x*y$ is a purple triangle); and the operator of $G_2$ does the same for the images (in this example, we can think of adding the matrices representing the images). Translating the definition to this example means that if we combine the features “red triangle” and “blue triangle” (e.g., both are vectors with two elements, indicating RGB color and shape) and mapping this feature vector to an image is equivalent to combining the images of a blue and a red triangle.
Homomorphism
We already have defined isomorphisms that map between two groups with a bijective mapping, but this is a strong constraint as it requires that each element of $G_1$ is mapped to a single distinct element of $G_2$. Homomorphisms generalize these mappings by omitting the bijectivity constraint, leading to the definition:
The mapping between two groups $G_1, G_2$ is a homomorphisms if there is a mapping $\phi: G_1 \to G_2$ defined for each $x\in G_1$ such that $ \forall x,y \in G_1 : \phi(x)*\phi(y) = \phi(x*y)$, where * is the group operation.
Although we cannot invert a homomorphism generally the property $ \phi(x) * \phi(y) = \phi(x*y) $ still means that we preserve the group structure. In representation learning, we come across a similar concept when using Latent Variable Models (LVMs), where a small-dimensional latent vector describes high-dimensional observations (such as in the example above with factors such as color and shape as latents and the image as the high-dimensional observation).
When training Variational AutoEncoders (VAEs), it can happen that we experience posterior collapse, i.e., some elements in the latent space do not capture useful information, they are white noise. Intuitively, this relates to the concept of kernel (not the Linux one though):
The kernel of a homomorphism $\phi: G_1 \to G_2$ is the set of elements in $G_1$ that map to the unit element in $G_2$ and is denoted by $Ker(\phi)$.
We might think of the collapsed latents in VAEs as the kernel of the mapping to the observation space, since they do not contain information so they get mapped to a blurry image (whether that can be called a unit element is not trivial, but I am reasoning only on an intuitive level).
The image of $\phi$ is the set of elements in $G_2$ that can be produced by mapping elements of $G_1$ via the homomorphism $\phi(g_1) : g_1 \in G_1$ and is denoted by $Im(\phi)$.
In VAE language, these are the images you can generate.
Interestingly the quotient group $G/Ker(\phi)$ is isomorphic to $Im(\phi)$. That is, if we divide $G$ into cosets according to $Ker(\phi)$ (these are the clusters that “behave” in the same way w.r.t. the kernel) then this grouping is equivalent to taking the elements of $Im(\phi)$. Namely, each coset will be mapped to the same element of $Im(\phi)$. This means that the latent space can be divided into specific clusters yielding the same image; the importance of which is that it defines a sort of symmetry/invariance in the latent space showing that some changes in the latents do not affect the generated image.
Summary
This post was quite heavy introducing a lot of mathematical concepts and notation, but hopefully it provided some intuition why abstract algebra is useful for the geometry of deep learning. Namely, it describes symmetries, and that is what we are after.
]]>