Cover your bases.

The Machine Learning Interview Checklist

Generally speaking, interviews for Ph.D. positions, internships in machine learning are generally structured into three parts:

• mathematics,
• programming, and
• machine learning. This is sometimes accompanied by a presentation of a paper or your work. In the following, I collected the most frequent topics you will potentially encounter.

Mathematics

It is not all you need for a machine learning interview, but reading and comprehending each concept in the freely available Mathematics for Machine Learning book is what can lay the foundations on the math and fundamental machine learning side. Regarding mathematical concepts, you need to be fluent at least in:

• Linear algebra
• Probability
• Analysis
• Optimization

Linear algebra

Since neural networks consist of matrices and tensors, it is essential to be aware of the corresponding operations—knowledge of matrices is a must, tensors are a nice-to-have, but you need to have an intuition that tensor can be thought of “generalized matrices into higher dimensions”. Matrix knowledge includes how linear equation systems and matrices correspond, what are the computational aspects of matrix algebra (cost) and how matrices can express linear transformations—unfortunately, bonus points cannot be collected for knowing the eponymous film series.

Linear equations can be thought as (intersecting) hyperplanes in a vector space, so characterization of a vector space is essential. When we connect matrices—what we do since they can describe the equation system—to vector spaces, we also want to measure angles and distances, so being aware of norms, inner products is also a must.

When we talk about matrices, decompositions such as Singular Value Decomposition (SVD) and Principal Component Analysis (PCA) cannot be neglected. Here the key is to understand what these decompositions mean, and also what we can do with them (low-rank approximations and even unsupervised representation learning in simple cases).

This figure from the MML book can be very helpful to comprehend all things matrix philogeny: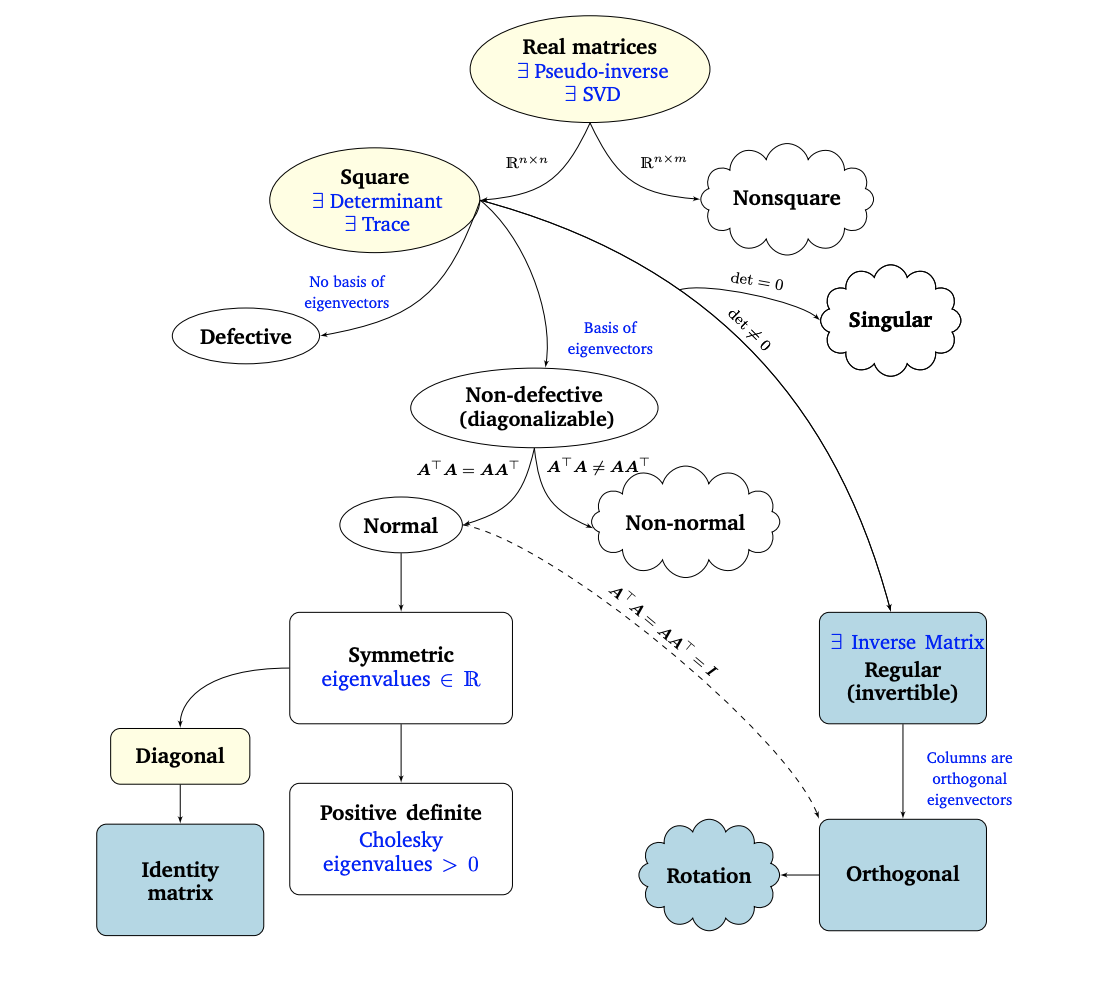

Checklist

• matrix operations
  • multiplication (non-commutative, exceptions exist)
  • inverse
  • Moore-Penrose pseudoinverse
  • transpose
  • conjugate
  • adjoint
  • trace
  • determinant
    • connection to invertibility
    • geometric interpretation
• matrix properties and their connections
  • definiteness
  • (anti-)symmetry
  • square matrices
  • similar matrices
  • constructing (anti-)symmetric matrices from a general matrix
  • orthogonal matrices (rotations)
  • matrices and linear transformations
• matrix decompositions
  • low-rank approximations
  • spectral decomposition
  • diagonalization
  • Principal Component Analysis (PCA)
  • Singular Value Decomposition (SVD)
  • Cholesky
  • QR
  • LU
  • Eigendecomposition
    • characteristic polynomial
• equation systems
  • relation to matrices
  • classification based on number of solutions
  • geometric interpretation (intersection of hyperplanes)
  • Gaussian elimination
  • underdetermined problems
  • overdetermined problems
  • approximate/least-squares solution (when no exact solution exists)
  • geometric and algebraic multiplicity (connection to eigenvalue problem)
• inner products
  • meaning (“orthogonality”)
• $p$-norms
  • metrics
  • triangle inequality
  • Cauchy-Schwarz inequality
• vector spaces
  • inner product spaces, normed spaces
  • subspaces
  • linear (in)dependence
  • orthogonal bases
  • span
  • orthogonal projection
  • orthogonal complement
  • orthogonalization (Gram-Schmidt)
  • image space
  • kernel/null space

Probability

Understanding Bayes’s theorem is the bread and butter for several machine learning algorithms. Besides helping with the Monty Hall Problem, it is a fundament of a broad range of methods aiming to infer unmeasured quantities. However, not everything is Bayesian estimation: Maximum Likelihood and Maximum A Posterior methods are also frequently used. Factorization, independence and the latter’s relation to (un)correlatedness are further essential concepts, since assumptions on distributions generally are about them. To juggle with distributions, we need to distinguish them by names such as marginal, conditional, or joint; to manipulate them (read: to use Bayes’s theorem), we need the Sum and teh Product rules. Be also aware of the special role of the Gaussian, and exponential families (to get conjugate priors for Bayes estimation, leading to closed-form solutions) can also become handy. Staying with the Gaussian, its prominence in the Central Limit Theorem is the basis for using the Gaussian assumption on distributions. When we want to transform probability densities, then the change of variables formula will be our tool. There are properties (sufficient statistics) that can describe distributions concisely, the mean and variance are such (they are sufficient to describe a Gaussian) and they have interesting properties. It is also worth knowing that they are instantiations of (central) moments, which can be thought as a general family of descriptors for probability distributions. A pinch of information theory, i.e., quantities related to the information content of a random variable, are used in several fields of machine learning. (Differential) Entropy is the most important concept, but cross entropy and mutual information are also essential.

Checklist

• Probability mass function (pmf)
• Probability density function (pdf)
• Cumulative density function (cdf)
• Sufficient statistics
• Mean
• (Co)variance
• Correlation
• (Conditional) Independence
• Uncorrelatedness vs Independence
• Factorization of a joint distribution
• Conditional distribution
• Marginal distribution, marginalization
• Sum rule
• Product rule
• Bayes’s Theorem
  • likelihood
  • prior
  • posterior
  • evidence (marginal likelihood)
• Relation of probabilistic estimation methods
  • Bayes estimation (full Bayes)
    • prior predictive distribution
    • posterior predictive distribution
  • Maximum A Posteriori (MAP) estimation
  • Maximum Likelihood (MLE) estimation
• Markov factorization, Markov property
• Gaussian distribution with special properties
• Central Limit Theorem (CLT)
• Exponential families (conjugacy)
• Change of variables formula
• Information theory
  • (Differential) entropy
  • Cross entropy
  • Mutual information

I would also recommend some online courses, particularly the Bayesian Statistics Specialization on Coursera - with flashcards for the first two courses available on my blog; here for the first, and here for the second course. Additionally, there are related aspects in the Probabilistic Graphical Methods Specialization on the same website, with flashcards by yours truly for PGM1, PGM2, and PGM3.

Analysis

Analysis is mostly a tool for optimization in the context of machine learning - if you happen to be a theorist, it can be much more, but let’s stick to the fundamentals. Knowing what the derivative is, what it means (also for vector valued functions) is essential to understand optimization methods and the Taylor approximation. So the Jacobian and the Hessian should be a trusted acquaintance. The former is also required for the change of variables formula mentioned above.

Checklist

• Differentiation
  • Total differential
  • Partial derivative
  • Directional derivative
  • Gradient
• Jacobian matrix
• Hessian matrix
• Taylor series
• Taylor approximation
• Differentiation identities
  • Chain rule
  • Quotient rule
  • Composite function

Optimization

Since machine learning evolves around mostly gradient-based optimizers, Stochastic Gradient Descent (SGD) makes the top of the list. Taking a step back, you should be aware about the family of first-order methods, and why they are popular (computationally low cost). But beware of the caveats: local optima, setting the step size and co. So as a follow-up, ponder why second-order methods should (they are aware of the curvature) and should not (calculating the Hessian is costly) be used. When we need to incorporate prior knowledge/constraints, then a Lagrange-multiplier will come handy. It is also good to know why we love convex optimization (i.e., to wonder about the good old days when problems were convex, as ML problems will not be convex in most cases). It might also be useful to know about the Karush-Kuhn-Tucker (KKT) conditions, which collect necessary conditions for the solutions of constrained optimization problems, including problems with inequality constraints in nonlinear programs (a synonym for optimization problem). To transition towards ML-related topics, here you should know optimizers such as ADAM, Nesterov momentum, or RMSProp - the key is they use an averaging procederure (‘momentum’) to incorporate previous update(s). As a final twist, knowing conceptually how modern ML frameworks implement gradient calculation (automatic differentiation) also belongs to the good-to-know facts.

• First-order methods
  • Gradient descent (ascent)
  • Stochastic Gradient Descent (SGD)
  • Full-batch vs Mini-batch
• Second-order methods
  • Why they are useful for convex problems
  • Geometric interpretation (using curvature)
  • Drawbacks (expensive)
• Gradient conditions for (unconstrained) minima
  • First-order (necessary)
  • Second-order (sufficient)
• Karush-Kuhn-Tucker (KKT) conditions
• More advanced (ML) optimizers
  • Momentum
  • Adam
  • RMSProp
• Automatic differentiation (concept)
  • forward pass
  • backward pass

The hilariously-titled All the Math You Missed (But Need to Know for Graduate School) also looks promising, but as far as I can tell from skimming it, it is for the next level.

Machine learning

Fundamentals

The categories of machine learnin (supervised, unsupervised, and reinforcement learning are the three main categories, but self-supervised and semi-supervised learning also belongs) are a must.

For supervised methods, classification and regression are the categories you need to be aware of, including what loss functions (cross entropy vs mean squared error) are used. Additionally, the Support Vector Machine (SVM) with its hinge loss also often comes up. Flavors of regression (linear, polynomial) are also prevalent.

For unsupervised, PCA from linear algebra is a trusted friend, but it needs to be accompanied by k-means and Gaussian Mixture Models (GMMs), including how the latter two relate to each other (GMM is “soft” k-means).

Reinforcement learning: model-free and model-based, offline and online RL are useful categories to keep in mind. To my best knowledge, these will mostly come up during an interview if you want to work in the field of reinforcement learning.

Nitty-gritty details of what coulf (and will) go wrong during training and how to fight them also comprises the essential toolbox of a machine learning engineer/researcher, including data preparation, architecture design. This is to find a trade-off between underfitting and overfitting.

Checklist

• Categorization
  • Supervised
    • Classification
      • Support Vector Machines (SVMs)
        • margin
        • support vector
      • loss functions
        • Cross Entropy
        • Hinge Loss (SVM)
    • Regression
      • Mean Squared Error
  • Unsupervised
    • Principal Component Analysis (PCA)
    • k-Means
    • Gaussian Mixture Models (GMMs) + Expectation-Maximization (EM)
    • (Variational) Autoencoders
  • Reinforcement Learning
  • Semi-supervised Learning
  • Self-supervised Learning
• Bias-variance trade-off
  • Overfitting
    • Reasons
    • Solutions
  • Underfitting
    • Reasons
    • Solutions
• Exploration vs exploitation dilemma
• Cross-validation
• Latent variable models
• Exploding and vanishing gradients
  • Batch Normalization
  • Gradient clipping
  • Residual Networks (ResNets)
  • LSTM
• Data preprocessing (e.g., whitening)
• Data augmentations

Specifics

Of course, they are the field-specific knowledge like ResNets, Transformers, CNNs for computer vision. Here generally what is expected to provide a high-level, intuitive understanding of modern/state-of-the-art methods, but it is generally not required to comb through arXiv digest daily.

Programming

Know machine learning frameworks (PyTorch and TensorFlow are the big two, but JAX is on the rise as far as I can tell), and you can shine if you can compare them. If you use any of those, then you should prepare to state why you use it.

Additionally, there are Easter eggs where you can show your commitment—even better if you can showcase it on your GitHub profile. I am talking about the dreaded triad of

• documentation,
• unit testing, and
• Continuous Integration As an extra, you can add in knowledge about container-based frameworks such as Singularity or Docker - most cluster infrastructures are based on those.

For Python, realpython.com is my go-to resource, you can learn about all these concepts there.

Checklist

• Frameworks
  • PyTorch
  • TensorFlow
  • Keras
  • JAX
• Best practices
  • Documentation
  • Unit testing
  • Continuous Integration
• Container-based tools
  • Singularity
  • Docker

Your two cents

Let it be research or programming, be honest and show your commitment and enthusiasm. If you have fields, you are interested in, say so. If you have a relevant project (plan), definitely talk about it.

Remember, think with the head of the interviewer.